(a-b)^3 formula proof 335773-A^3+b^3+c^3-3abc formula proof

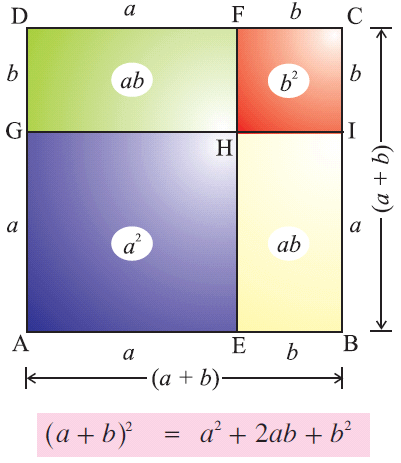
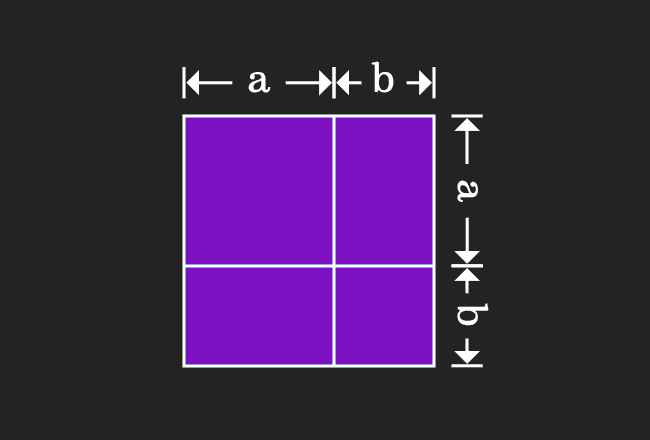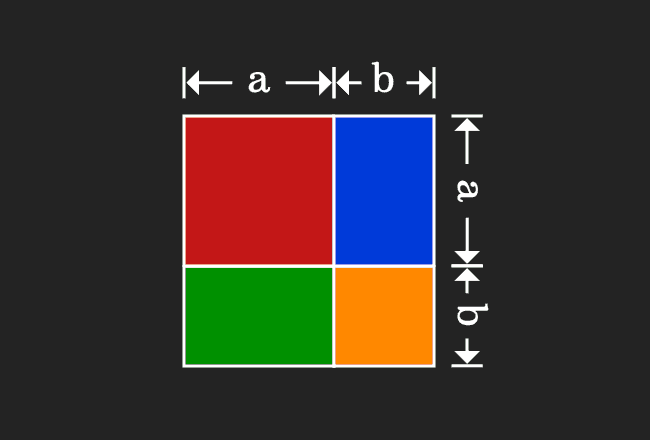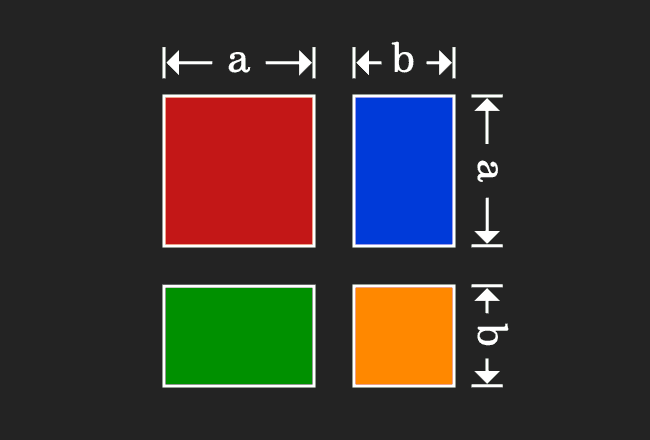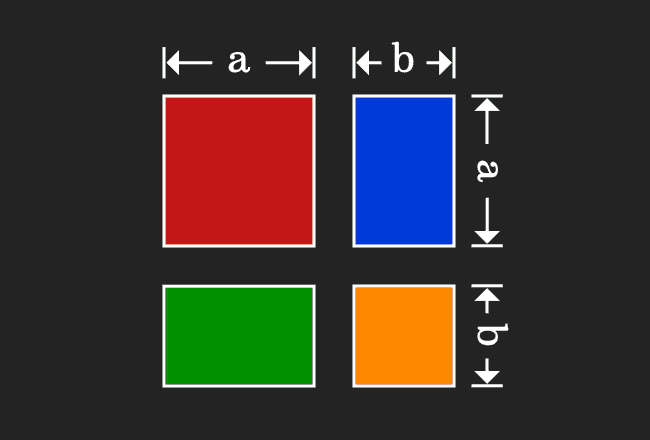
(ab) 2 = a 2 2ab b 2 (ab)(cd) = ac ad bc bd a 2 b 2 = (ab)(ab) (Difference of squares) a 3 b 3 = (a b)(a 2 ab b 2) (Sum and Difference of Cubes) x 2 (ab)x AB = (x a)(x b) if ax 2 bx c = 0 then x = ( b (b 2 4ac) ) / 2a (Quadratic Formula)And the quadratic formula was x The solutions would be equal to negative b plus or minus the square root of b squared minus 4ac, all of that over 2a And we learned how to use it You literally just substitute the numbers a for a, b for b, c for c, and then it gives you two answers, because you have a plus or a minus right thereA^3 – b^3 = (a – b)(a^2 ab b^2) a^3 b^3 = (a b)(a^2 – ab b^2) (a b)^3 = a^3 3a^2b 3ab^2 b^3 (a – b)^3 = a^3 – 3a^2b 3ab^2 – b^3

Binomial Theorem

A^3+b^3+c^3-3abc formula proof

A^3+b^3+c^3-3abc formula proof-Identity 3 Let A, B and C be sets Show that (A−B)−C = A−(B ∪C) Proof (A−B)−C = (A∩)−C set difference = (A∩)∩Cc set difference = A∩( ∩Cc) associative = A∩(B ∪C)c de Morgan's = A−(B ∪C) set difference Proof Let x ∈ (A − B) − C Then x ∈ (A − B) and x 6∈C by definition of set differenceVieta's formula relates the coefficients of polynomials to the sums and products of their roots, as well as the products of the roots taken in groups − b ± b 2 − 4 a c 2 a = 1 2 (− b a ± b 2 The proof of Vieta's formula follows by comparing coefficients in the equation

A B 2 A 2 B 2 2ab Proof With Calculation

A3 plus b3 plus c3 minus 3abc formula identity proof How is this identity obtained?Definition The longest side of the triangle is called the "hypotenuse", so the formal definition isProof Formula \(=> a^3 b^3 = (ab) (a^2 b^2 – ab) \) Verify \( a^3 b^3 \) Formula Need to verify \( a^3 b^3 \) formula is right or wrong put the value of a =2 and b=3 put the value of a and b in the LHS \( => a^3 b^3 = 2^3 3^3 \) \( = > a^3 b^3 = 8 27 = 35 \) put the value of a and b in the RHS \(=> (ab) (a^2 b^2 – ab) \) \(=> (23) (2^2 3^2 2 \times 3) \) \(=> (5) (4 9 – 6) \) \(=> (5) (7) = 35 \) Therefore \( LHS = RHS \) LHR = left hand side, RHS = right hand

Let's see how Taking RHS of the identity (a b c)(a 2 b 2 c 2 ab bc ca ) Multiply each term of first polynomial with every term of second polynomial, as shown belowA3 plus b3 plus c3 minus 3abc formula identity proof How is this identity obtained?Quadratic formula proof review This is the currently selected item Next lesson Strategizing to solve quadratic equations Sort by Top Voted Completing the square review Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organization Donate or volunteer today!

= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³(1) "b3" was replaced by "b^3" 1 more similar replacement(s) Step 1 Trying to factor as a Difference of Cubes 11 Factoring a 3b 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2 ab b 2) Proof (ab)•(a 2 abb 2) = a 3 a 2 b ab 2ba 2b 2 ab 3 = a 3 (a 2 bba 2)(ab 2b 2 a)b 3 = aWhat is A3 formula a³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³

Formula For A Plus B Whole Square

Solved Es 11 Formula The Euclidean Distance Ab Between Chegg Com

Two numbers r and s sum up to 5 exactly when the average of the two numbers is \frac{1}{2}*5 = \frac{5}{2} You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC(a b)^3 = a^3 3a^2b 3ab^2 b3 (a b)^3 = a^3 b^3 3ab(a b) (a – b)^3 = a^3 – 3a^2b 3ab^2 – b^3;Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots

How To Prove The Identiy A3 C3 3abc Math Polynomials Meritnation Com

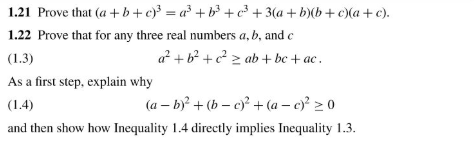
Solved 1 21 Prove That A B C 3 A3 C3 3 A B Chegg Com

2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 322 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32Bayes' theorem describes the probability of occurrence of an event related to any condition It is also considered for the case of conditional probability Bayes theorem is also known as the formula for the probability of "causes" For example if we have to calculate the probability of taking a blue ball from the second bag out of three different bags of balls, where each bag contains

A B 3 I E A Plus B Cube Formula Proof Ntse Algebraic Formulas Identity Geometrically Youtube

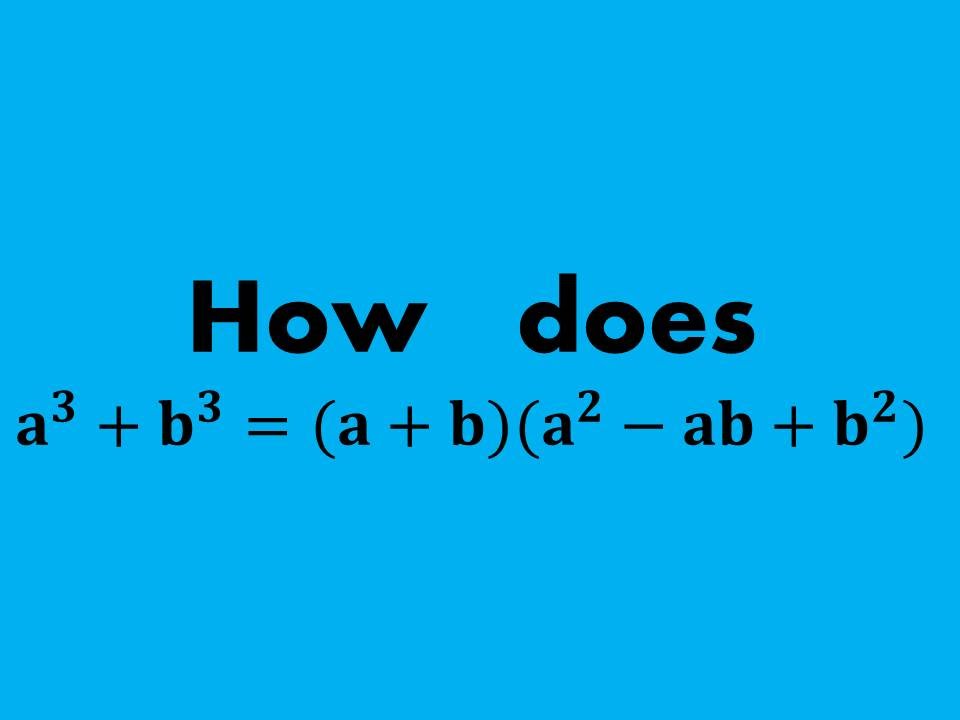
Proof How To Prove The Sum Of Two Cubes A 3 B 3 A B A 2 Ab B 2 Youtube

Solution This proceeds as Given polynomial (3a 2b) 3 represents the identity (a b) 3 Where a = 3a and b = 2b Now substitute values of a and b in the identity ie (a b) 3 = a 3 b 3 3ab (a b) and we get (3a 2b) 3 = (3a) 3 (2b) 3 3 (3a) (2b) (3a 2b) Expand the exponential forms and we getMath Doubts is a best place to learn mathematics and from basics to advanced scientific level for students, teachers and researchers Know more= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³

Difference Of Cubes Math Central

Vector Triple Product Definition Formula Proof Solved Problems

Let me help you with this formula in detail (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Proof (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) It can be written asLet's see how Taking RHS of the identity (a b c)(a 2 b 2 c 2 ab bc ca ) Multiply each term of first polynomial with every term of second polynomial, as shown belowA and b are the other two sides ;

A B 3 A3 3a2b 3ab2 But Why Math Formula Proof A B 3 And Algebraic Explanation Youtube

New Page 1

A 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcProof of sin(AB) identity Q1 is (sinB, cosB) PQ1 = 2–2sinAcosB2cosAsinB;Case 3 A is obtained from I by swapping two rows In this case det(A)=1, det(AB)=det(B), so again det(AB)=det(A)det(B) The proof is complete Notice that this proof shows, in particular, that the determinant of any elementary matrix is not zero To return to the theorem, click here A is invertible if and only if det(A) is not 0

What Is The Correct Formula Of Math A B 3 Math Quora

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

11 Factoring a 3b 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2 ab b 2) Proof (ab)•(a 2 abb 2) = a 3 a 2 b ab 2ba 2b 2 ab 3 = a 3 (a 2 bba 2)(ab 2b 2 a)b 3 = a 3 0 0b 3 = a 3b 3 Check a 3 is the cube of a 1 Check b 3 is the cube of b 1 Factorization is (a b) • (a 2 ab b 2)The answer is (ab)^3=a^33a^2b3ab^2b^3 It's easy to prove (ab)^3= =(ab)(ab)(ab)= =(a^2ababb^2)(ab)= =(a^22abb^2)(ab)= =a^3a^2b2a^2b2ab^2ab^2b^3A 3 B 3 Formula Source(s) https//shrinkim/a0r7w 0 0 What do you think of the answers?

Problem If A B C 0 Then Prove That B4 C4 2 B2 C2 Jsunil Tutorial Cbse Maths Science

Binomial Theorem

Proof How to Prove the Sum of Two Cubes a^3 b^3 = (ab) (a^2abb^2) YouTube Watch later Share Copy link Info Shopping Tap to unmute wwwdisneypluscom If playback doesn't beginLearn how to derive the expansion of a plus b whole cube formula in algebraic approach by the special product of three same binomials mathematicsWhen you take the square root of both sides of the equation, you need a plus or minus sign before the right side to show that the positive value squared equals (xb/2a)² and that the negative value squared equals (xb/2a)²The square root of x², for example, does not equal x but rather equals the absolute value of x, so the right side may be positive or negative

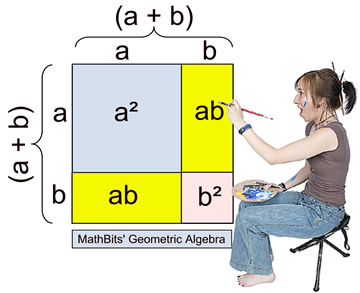
Special Binomial Patterns Mathbitsnotebook A1 Ccss Math

Heron S Formula Wikipedia

Notice, math(ab)^3=(ab)(ab)(ab)/math math=(ab)\underbrace{(ab)(ab)}/math math=(ab)(a(ab)b(ab)/math math=(ab)(a^2ababb^2)/math math=(aRegister for FREE at http//deltastepcom or download our mobile app https//bitly/3akrBoz to get all learning resources as per ICSE, CBSE, IB, Cambridge &Just like we expressed the geometric proof of expansion of quadratic formula we prove the expansion of (a b) 3 the expansion is (ab)³ = a³ 3a²b 3ab² b³

What Is The Formula Of Math A 3 B 3 Math Quora

How To Prove The Angle Sum Property Of A Triangle 7 Steps

Proof For events Bayes Once again, the answer can be reached without using the formula by applying the conditions to a hypothetical number of cases For example, if the factory produces 1,000 items, 0 will be produced by Machine A, 300 by Machine B, and 500 by Machine C Machine A will produce 5% × 0 = 10 defective items, Machine B 3%Just like we expressed the geometric proof of expansion of quadratic formula we prove the expansion of (a b) 3 the expansion is (ab)³ = a³ 3a²b 3ab² b³You can sign in to give your opinion on the answer Sign in buccinator 1 decade ago (a b)(a^2 a*b b^2) 6 2 Anonymous 1 decade ago a3 b3 = {(ab)3 (ab)23a3b2 3a2b3} 2 3 sushobhan Lv 6 1 decade ago (ab)(a^2 ab b^2) 3 0

What Is The Formula Of Math A 3 B 3 Math Quora

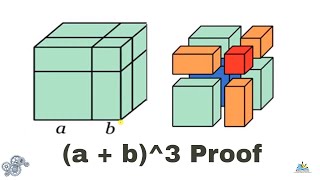
A B 3 I E A Plus B Cube Formula Proof Ntse Algebraic Formulas Identity Geometrically Youtube

Take a = 7 and b = 3 and find the values of both sides of the equation ( 1) ( a b) ( a − b) = ( 7 3) ( 7 − 3) = 10 × 4 = 40 ( 2) a 2 − b 2 = ( 7) 2 − ( 3) 2 = 49 − 9 = 40 ∴ ( 7 3) ( 7 − 3) = ( 7) 2 − ( 3) 2 = 40The answer is (ab)^3=a^33a^2b3ab^2b^3 It's easy to prove (ab)^3= =(ab)(ab)(ab)= =(a^2ababb^2)(ab)= =(a^22abb^2)(ab)= =a^3a^2b2a^2b2ab^2ab^2b^3(a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Practice Problems Problem 1 Expand (x 1) 3 Solution (x 1) 3 is in the form of (a b) 3 Comparing (a b) 3 and (x 1) 3, we get a = x b = 1 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 Substitute x for a and 1

Illustrations Of Formulas

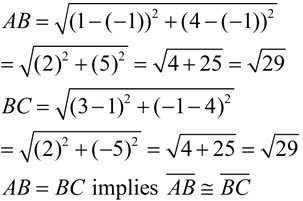
Coordinate Geometry Proofs Mathbitsnotebook Geo Ccss Math

RT = 2–2sin(AB) PQ1 = RT proves the required identity This proof in nubtrek holds for angle greater than 90° andThe proof will be the same as in our proof of Cauchy's theorem that \(g(z)\) has an antiderivative 442 Proof of Cauchy's integral formula We reiterate Cauchy's integral formula from Equation 521 \(f(z_0) = \dfrac{1}{2\pi i} \int_C \dfrac{f(z)}{z z_0} \ dz\)A b mod 2 and a b mod 3 Proof Suppose a b mod 6 Then 6j(a b), so 6x = (a b) for some x 2Z Then (a b) = 2(3x) = 3(2x), so (a b) is divisible by both 2 and 3 Then a b mod 2 and a b mod 3 Suppose a b mod 3 and a b mod 2 Then (a b) = 2x = 3y for some x;y 2Z From the rst expression, we see that (a b) is even, so y is even as well

Solved 1 Show That A B C A B C Required Method U Chegg Com

Solved L Let F Q Q Be A Function You Don T Have To Chegg Com

Algebra & Number Theory We provide the first steps towards a new relative trace formula proof of the celebrated formula of Waldspurger relating the square of a toric period integral on PGL 2 to the central value of an LfunctionThe proof ideas and also the proof ways can be described by pictures In addition the formulas themselves become more alive You take the drawing of the formula (ab)³=a³3a²b3ab²b³ from above and replace a by the difference ab Then the edges are (ab)b with different combinations (on the left)Answer a³ 3a²b 3ab² b³ Show more Rameshwar Lv 7 1 decade ago ( ab)^3 = ( a b)^2 (ab) = ( a^2 2ab b^2) ( a b ) = a^3 3a^2b 3b^2a b^3 = a^3 3ab ( a b) b^3 ans in

Caml Types And Intuitionistic Logic A Project By Dale Miller Dale Miller Inria Fr 1 Goal The Goal Of This Project Is To Use A Theorem Prover For Propositional Intuitionistic Logic In Order To Answer Questions About A Collection Of Caml Types In Particular If One Is

Www Math Only Math Com Proof Of Compound Angle Formula Sin Alpha Plus Beta Html

2 sine formula a/Sin A=b /Sin B=c /Sin C Proving the Sine Rule Alisoncom 3 cosine formula a 2 = b 2 c 2 – 2 bc cos A Proving the Cosine Rule Alisoncom 4 cos (A–B) = cos A cos B sin A sin B Proof from Youtube KeysToMaths1 5 cos (AB) = cos A cos B – sin A sin B Proof from Youtube KeysToMaths1The area of a trapezoid whose bases are 'a' and 'b' and whose height is 'h' is A = ½ (a b) h If one of the bases (say 'a'), height, and area are given, then we will just substitute these values in the above formula and solve it for the missing base (a) as follows A = ½ (a b) h Multiplying both sides by 2, 2A = (a b) h Dividing bothProof of Pythagorean triples a 2 b 2 = c 2 (1) then (a, b, c) is a Pythagorean triple If a, b, and c are relatively prime in pairs then (a, b, c) is a primitive Pythagorean triple Clearly, if k divides any two of a, b, and c it divides all three

Using Distance Formula Prove That The Points A 4 3 1 B 5 7 6 And C 3 1 8 Are Collinear Mathematics Topperlearning Com Fczt7f877

What Is The Formula Of Math A 3 B 3 Math Quora

1=2 A Proof using Beginning Algebra The Fallacious Proof Step 1 Let a=b Step 2 Then , Step 3 , Step 4 , Step 5 , Step 6 and Step 7 This can be written as , Step 8 and cancelling the from both sides gives 1=2 See if you can figure out in which step the fallacy lies(ab) 2 = a 2 ba ba b 2 ie (ab) 2 = a 2 2ab b 2 Hence Proved This simple formula is also used in proving The Pythagoras Theorem Pythagoras Theorem is one of the first proof in Mathematics In my view, in mathematics when a generalized formula has been framed there will be a proof to prove and and this is my small effort toIt is called "Pythagoras' Theorem" and can be written in one short equation a 2 b 2 = c 2 Note c is the longest side of the triangle;

Proof Of The Formula For A 3 B 3

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Heron's formula to find the area of a triangle with given lengths of all three sides Know the formulas to find the area of the quadrilateral and all types of triangles using Hero's formula with solved examples at BYJU'S

What Is The Formula Of Math A 3 B 3 Math Quora

A B 3 A3 3a2b 3ab2 Hindi Herunterladen

Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2

Using Section Formula Prove That The Three Points 4 6 10 2 4 6 And 14 0 2 Are Collinear

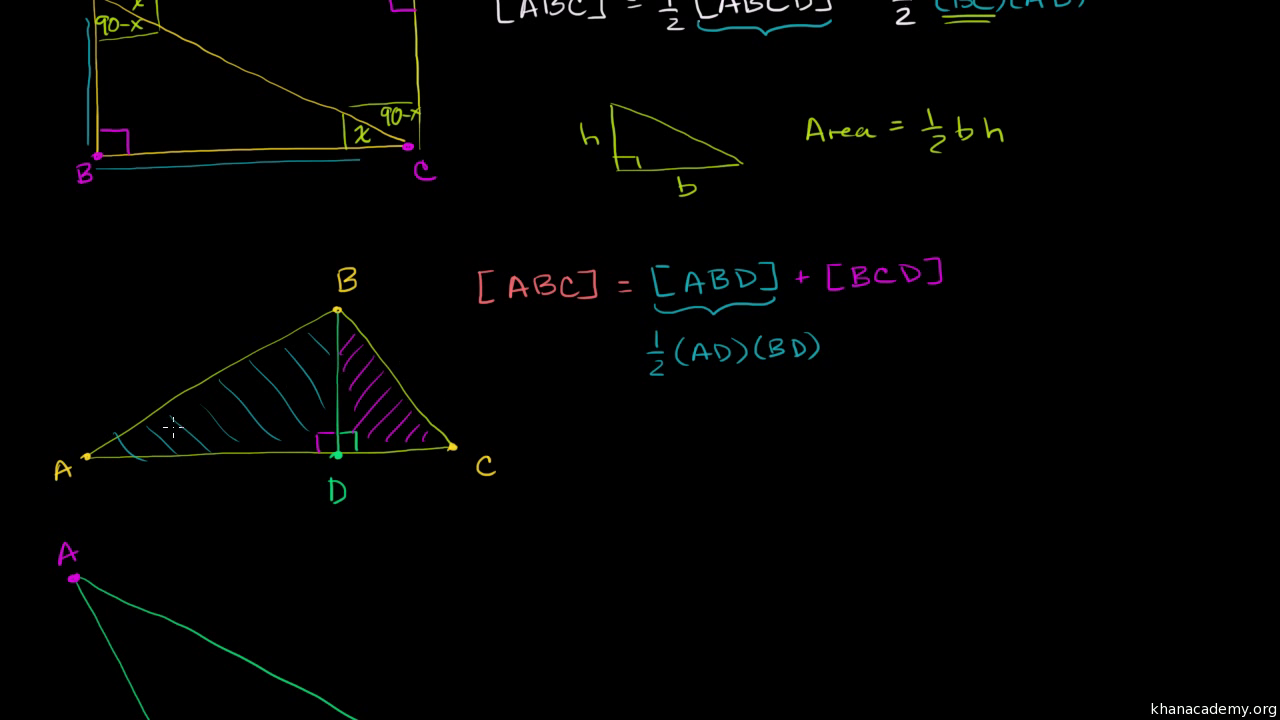
Area Of Triangle Proof Video Khan Academy

Ex 10 1 9 Without Using Distance Formula Show That Ex 10 1

Why Is A B 2 B2 2ab

Q Tbn And9gcsxj6nch9jkvcgw2jprateqxk Fehjaprpo Txh0pvbjcp 2po Usqp Cau

Quadratic Formula Calculator

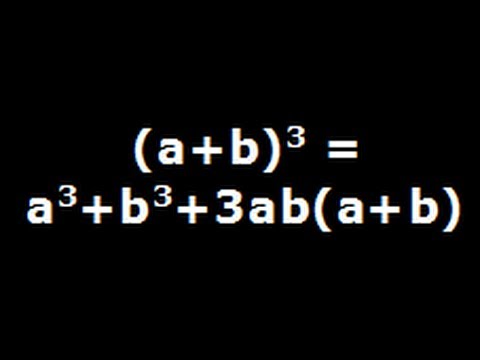
A Plus B Cube Algebra Identity Explained Step By Step Youtube

A B 2 A 2 B 2 2ab Proof With Calculation

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy

A Cube Minus B Cube A 3 B 3 Geometrical Explanation And Derivation Of Algebra Identity Youtube

Proof Of A B Formula In Geometric Method

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Pythagorean Theorem And Its Many Proofs

Spot The Math Errors Skulls In The Stars

What Is The Formula Of Math A B 3 Math Quora

Spot The Math Errors Skulls In The Stars

Algebraic Identities Proofs Solved Examples Practice Questions

Yismxplusc Geometric Proof Of The Cubic Formula A B 3

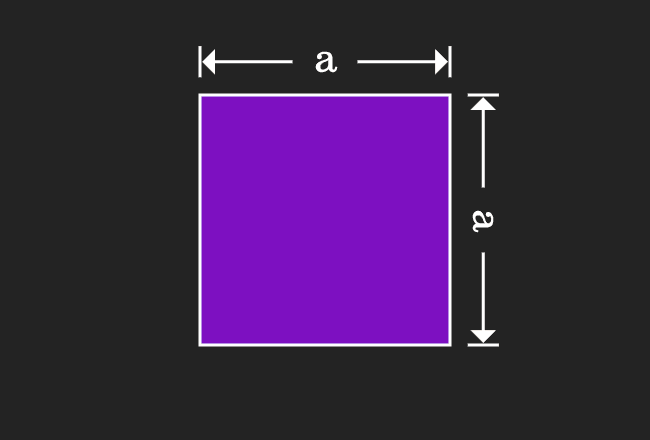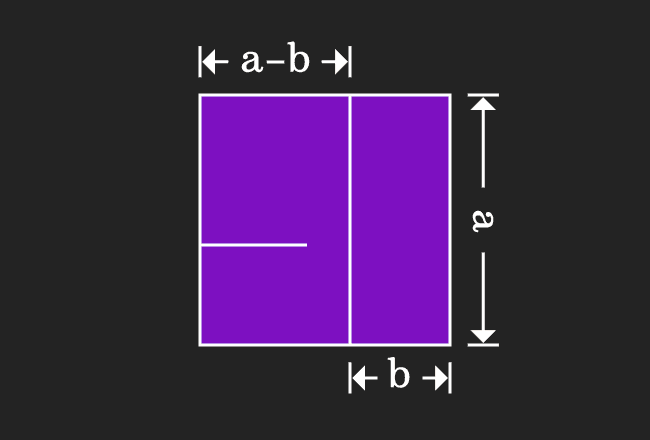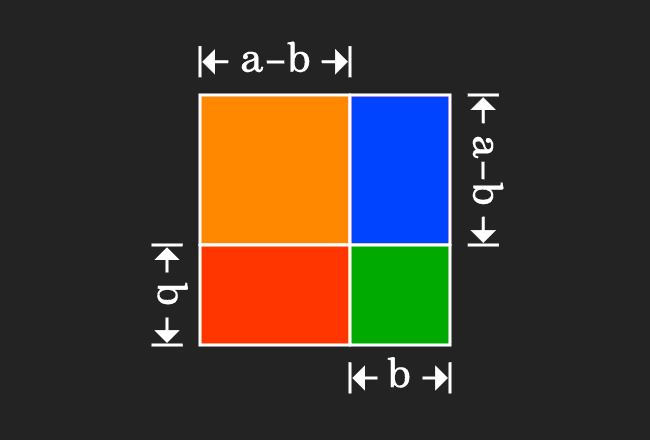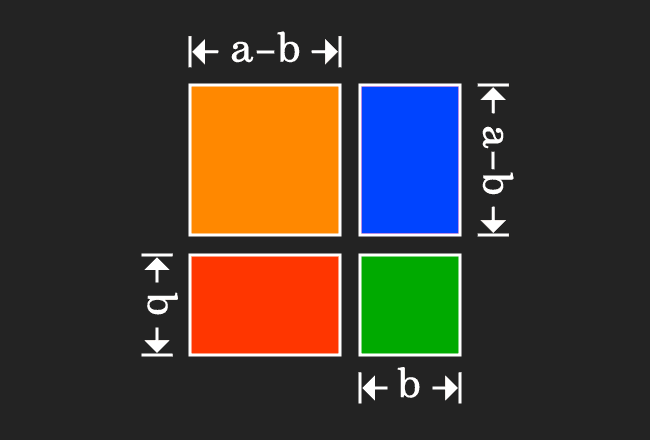
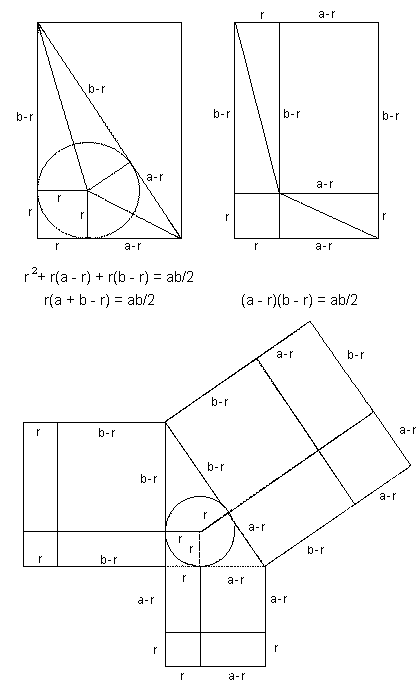
Proof Of A B Formula In Geometric Method

Firststep By Rishabh Singla Geometrical Visual Proof Of The Famous Formula A B 2 A 2 B 2 2 A B

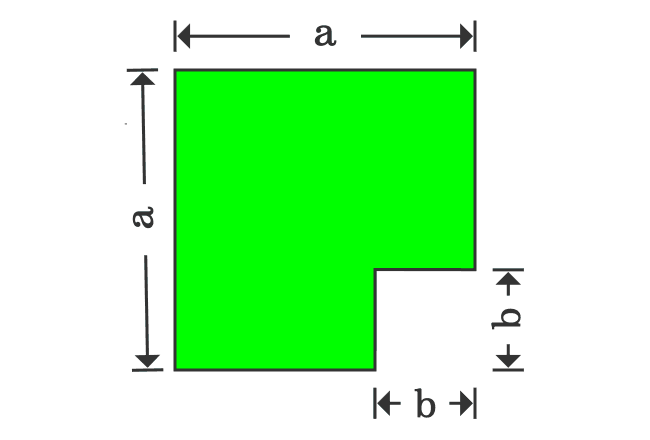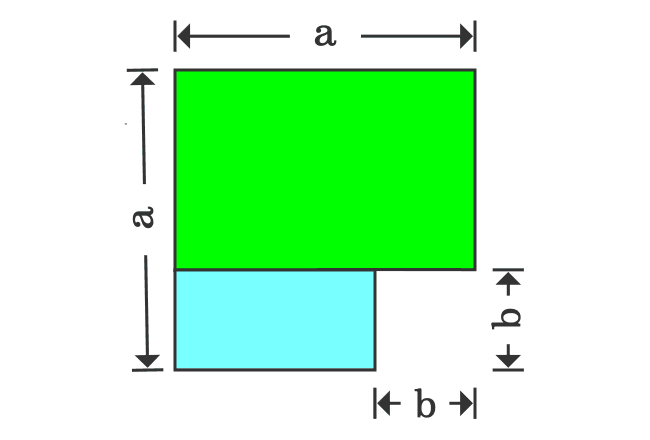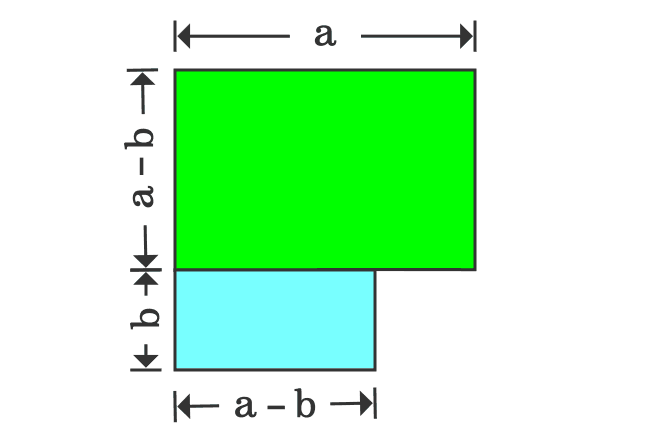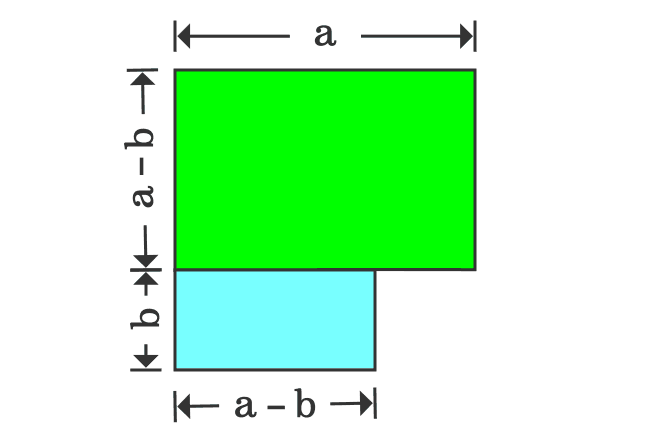
Proof Of A B Formula In Geometric Method

Lesson 5 3 Multiplying Polynomials Objectives Students Will Multiply Any Polynomials Multiply Binomials Using Foil Square A Binomial Multiply The Sum Ppt Download

If A B C Are In Continued Proportion Prove That A 3 B 3 C 3 A 2 B 2 C 2 1 A 3 1 B 3 1 C 3 Mathematics Topperlearning Com 8p157uuu

Give Me The Proof Of A 3 B 3 Mathematics Topperlearning Com Zcc4adww

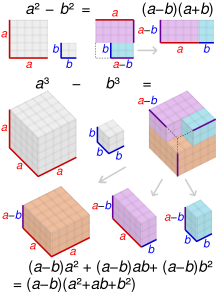
Difference Of Two Squares Wikipedia

Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9

If Sin 4 Theta A Cos 4 Theta B 1 A B Prove Sin 8theta A 3 Cos 8 Theta B 3 1 A B 3 Mathematics Topperlearning Com D4l80mdd

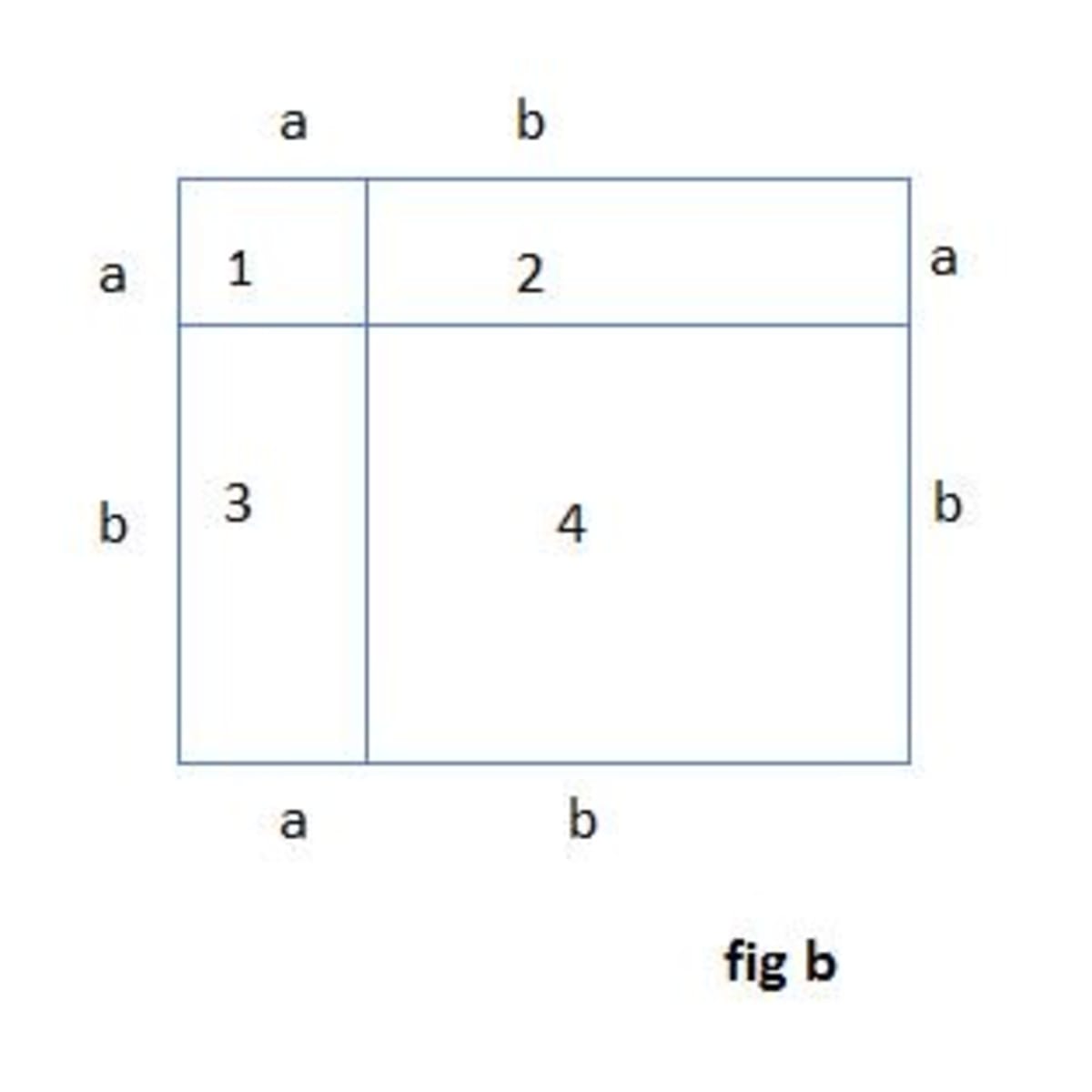
Why A B 2 B2 2ab Owlcation Education

What Is The Formula For Math A 3 B 3 Math Quora

Simple Proof Of A B A 3a B 3ab B A B 3ab A B And A B A 3a B 3ab B A B 3ab A B Youtube

If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline

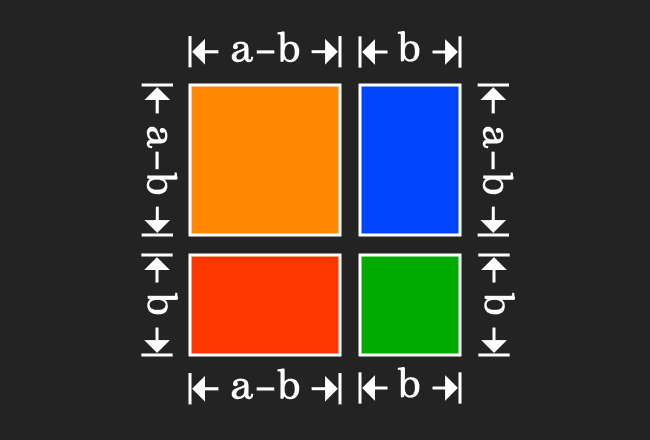
Proof Of A B Formula In Geometric Method

If A B C 0 Then A 3 B 3 C 3 0 How Quora

Illustrations Of Formulas

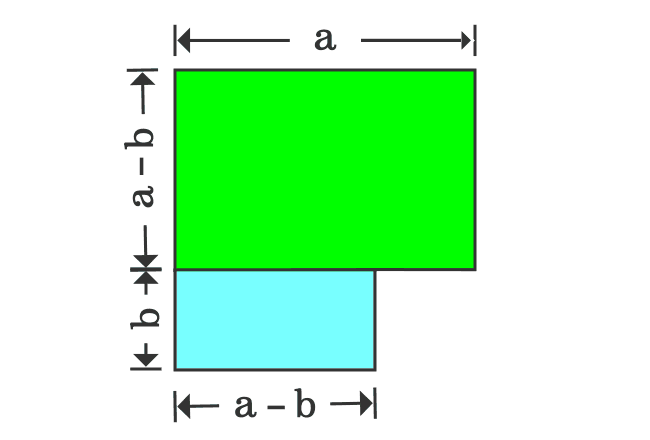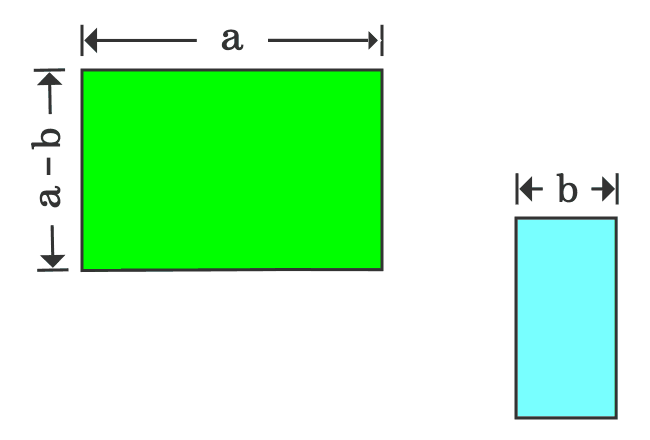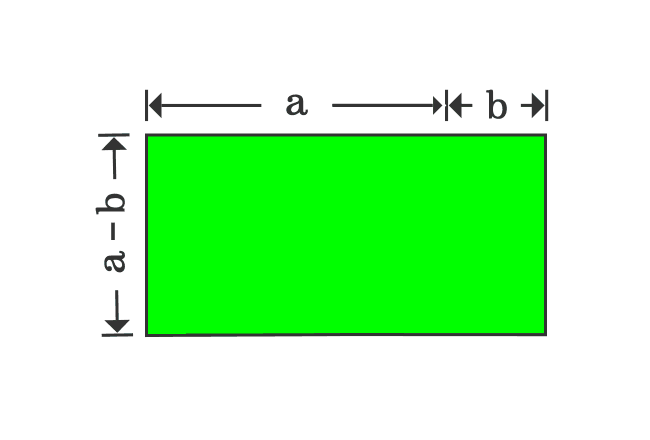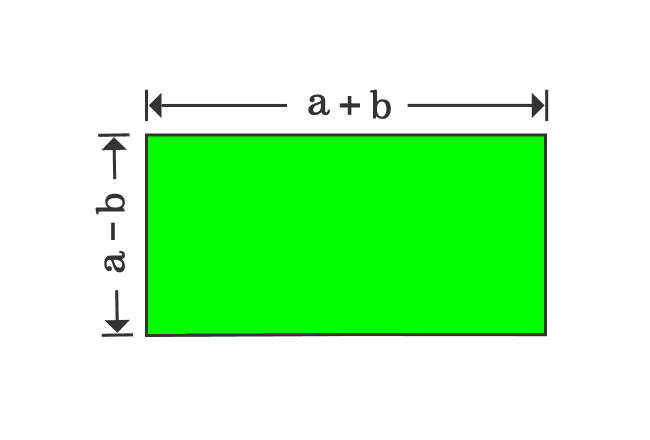
Proof Of A B Formula In Geometric Method

Algebra Sleuth Proof That 1 2 Activity Education Com

Answer Needed Asap What Is The Reason For Statement 3 In This Proof A Using Point Slope Brainly Com

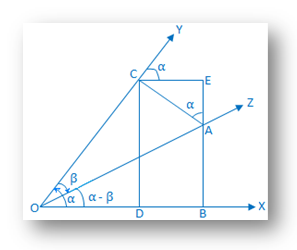
Proof Of Compound Angle Formula Cos A B Trigonometric Identities

Theorem Wikipedia

Solution Given Db Is Not Congruent To Ac To Prove Ab And Cd Do Not Bisect Each Other Drawing 400 400 6 6 6 6 Line 4 4 4 5 Line 5 4 5 4 Line 4 4 5 4 Line 5 4 4 5

A B 3 Geometric Proof

A B A B 3ab A B And A B A B 3ab A B Formula Proof By Easy Method Youtube

If If A B C Are All Non Zero And A B C 0 Prove That B2 Ca C2 Ab 3 Mathematics Topperlearning Com 2jnu5w66

Algebra Sleuth Proof That 1 2 Activity Education Com

A B 3 Proof

A Minus B Cube Or A Minus B Whole Cube A B 3 Geometric Explanation Derivation Youtube

Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline

Derivation Of Formula For A B 3

Algebraic Identities Proofs Solved Examples Practice Questions

Example 8 Using Section Formula Prove That Three Points

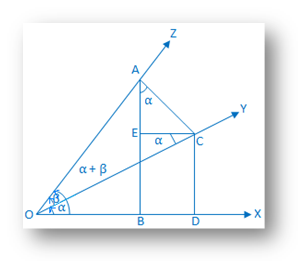
Proof Of Compound Angle Formula Cos A B Addition Formulae

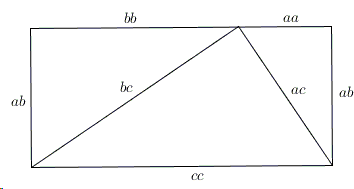
Pythagorean Theorem And Its Many Proofs

Illustrations Of Formulas

Prove A B C 3 A 3 B 3 C 3 3 A B B C C A Mathematics Topperlearning Com 9j3ovqff

Geometrical Proof Of A B 3 Brainly In

What Is The Correct Formula Of Math A B 3 Math Quora

Heron S Formula Area Of A Triangle Knowing Lengths Of 3 Sides Algebraic Proof Steemit Algebraic Proof Formula Proof

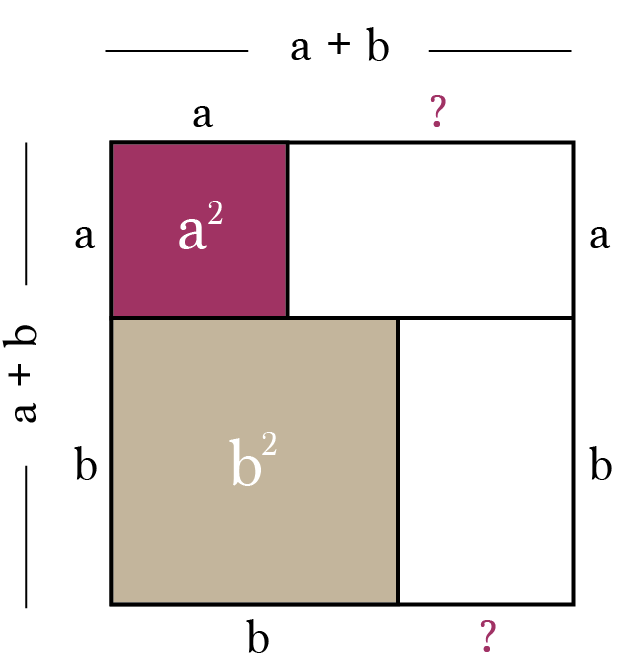
Visual Proof Of The Pythagorean Theorem By Brett Berry Math Hacks Medium

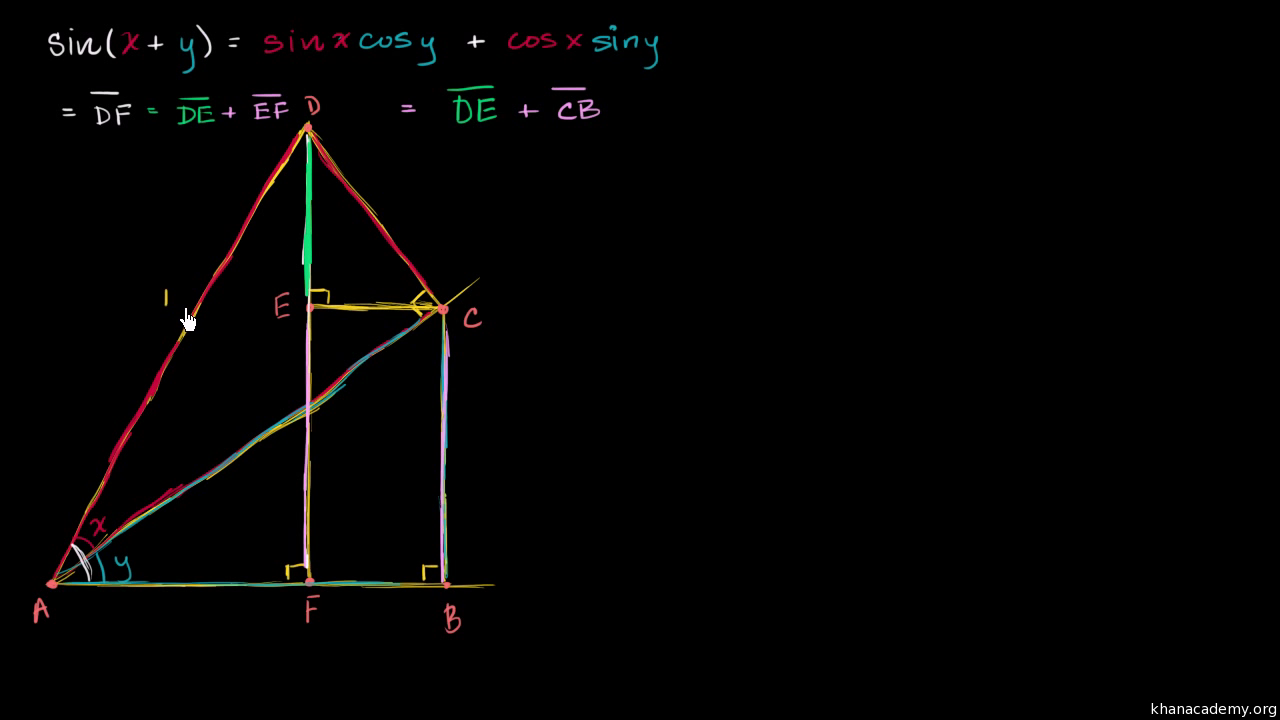
Proof Of The Sine Angle Addition Identity Video Khan Academy

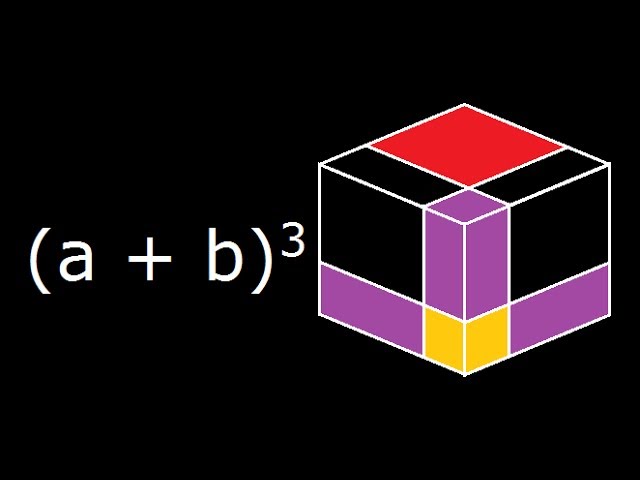
A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube

Algebraic Identities For Class 8 Formulas And Proofs

Q Tbn And9gcsjdrnx7bzqtlocyzksajkrzoljxhqicxqu10lfrwznup Pf Ff Usqp Cau

Q Tbn And9gct67k0tylvuuc5ijp5kzjbldpp6tryb6uwckkmjhjh6z6 Iamg0 Usqp Cau

What Are Various Forms To Write A B C A Whole Cube Quora

Proof Of A B 3 A3 3a2b 3ab2 Proof Of A B 3 Formula Youtube

New Page 1

Search Q A 5e3 2bb 5e3 Tbm Isch

What Is The Formula Of Math A B 3 Math Quora

Questions About The Proof Of The Cosine Of A Subtraction Math

Cubic Equation Wikipedia

Incoming Term: (a+b)^3 formula proof, (a+b+c)^3 formula proof, a^3+b^3+c^3-3abc formula proof,